Features catalogs tutorial (features)¶
This notebook give some insights about the data stored in all the features types catalogs.
[1]:
# import the module and instance the client
import carpyncho
client = carpyncho.Carpyncho()
Now we download one features catalog
[2]:
df = client.get_catalog("b214", "features")
df.sample(3)
b214-features: 159MB [01:06, 2.40MB/s]
[2]:
| id | cnt | ra_k | dec_k | vs_type | vs_catalog | Amplitude | Autocor_length | Beyond1Std | Con | ... | c89_jk_color | c89_m2 | c89_m4 | n09_c3 | n09_hk_color | n09_jh_color | n09_jk_color | n09_m2 | n09_m4 | ppmb | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 246230 | 32140000304888 | 66 | 281.886621 | -24.814519 | 0.18675 | 1.0 | 0.287879 | 0.0 | ... | 0.790576 | 15.292760 | 15.256852 | 0.274868 | 0.188890 | 0.602440 | 0.791330 | 15.479110 | 15.486869 | 2.341868 | ||
| 375156 | 32140000459091 | 44 | 281.626075 | -24.136333 | 0.27050 | 1.0 | 0.431818 | 0.0 | ... | 0.475020 | 16.945470 | 16.877186 | 0.682651 | -0.076031 | 0.551810 | 0.475779 | 17.051519 | 17.072001 | 4.627671 | ||
| 264628 | 32140000328959 | 39 | 281.817479 | -24.701575 | 0.28200 | 1.0 | 0.333333 | 0.0 | ... | 0.498984 | 16.798042 | 16.762198 | 0.305437 | 0.071062 | 0.428715 | 0.499777 | 16.923741 | 16.932339 | 0.928964 |
3 rows × 73 columns
The columns of this catalog are
[3]:
print(list(df.columns))
['id', 'cnt', 'ra_k', 'dec_k', 'vs_type', 'vs_catalog', 'Amplitude', 'Autocor_length', 'Beyond1Std', 'Con', 'Eta_e', 'FluxPercentileRatioMid20', 'FluxPercentileRatioMid35', 'FluxPercentileRatioMid50', 'FluxPercentileRatioMid65', 'FluxPercentileRatioMid80', 'Freq1_harmonics_amplitude_0', 'Freq1_harmonics_amplitude_1', 'Freq1_harmonics_amplitude_2', 'Freq1_harmonics_amplitude_3', 'Freq1_harmonics_rel_phase_0', 'Freq1_harmonics_rel_phase_1', 'Freq1_harmonics_rel_phase_2', 'Freq1_harmonics_rel_phase_3', 'Freq2_harmonics_amplitude_0', 'Freq2_harmonics_amplitude_1', 'Freq2_harmonics_amplitude_2', 'Freq2_harmonics_amplitude_3', 'Freq2_harmonics_rel_phase_0', 'Freq2_harmonics_rel_phase_1', 'Freq2_harmonics_rel_phase_2', 'Freq2_harmonics_rel_phase_3', 'Freq3_harmonics_amplitude_0', 'Freq3_harmonics_amplitude_1', 'Freq3_harmonics_amplitude_2', 'Freq3_harmonics_amplitude_3', 'Freq3_harmonics_rel_phase_0', 'Freq3_harmonics_rel_phase_1', 'Freq3_harmonics_rel_phase_2', 'Freq3_harmonics_rel_phase_3', 'Gskew', 'LinearTrend', 'MaxSlope', 'Mean', 'Meanvariance', 'MedianAbsDev', 'MedianBRP', 'PairSlopeTrend', 'PercentAmplitude', 'PercentDifferenceFluxPercentile', 'PeriodLS', 'Period_fit', 'Psi_CS', 'Psi_eta', 'Q31', 'Rcs', 'Skew', 'SmallKurtosis', 'Std', 'StetsonK', 'c89_c3', 'c89_hk_color', 'c89_jh_color', 'c89_jk_color', 'c89_m2', 'c89_m4', 'n09_c3', 'n09_hk_color', 'n09_jh_color', 'n09_jk_color', 'n09_m2', 'n09_m4', 'ppmb']
Where
- id (ID): This is the unique identifier of every light curve. If you want to access all the points of the lightcurve of a source wiht any id, you can search for the same value of a
bm_src_idin thelcof the same tile of the features catalog. - cnt (Count): How many epochs has the lightcurve.
- ra_k: Right Ascension in band \(K_s\) of the source in the first epoch.
- dec_k: Declination in band \(K_s\) of the source in the first epoch.
- vs_type (Variable Star Type): The type of the source if is a variable star tagged with the OGLE-III, OGLE-IV and VIZIER catalogs; or empty if the source has no type.
- vs_catalog (Variable Star Catalog): From which catalog the vs_type was extracted.
All the other columns (Except the last 13) are the features itself And can be consulted here https://feets.readthedocs.io/en/latest/tutorial.html#The-Features
Finally the reddening free features are:
c89_c3: \(C3\) Pseudo-color using the cardelli-89 extinction law.
c89_ab_color: Magnitude difference in the first epoch between the band \(a\) and the band \(b\) using the Cardelli-89 extinction law. Where \(a\) and \(b\) can be the bands \(H\), \(J\) and \(K_s\).
c89_m2 and c89_m4: \(m2\) and \(m4\) pseudo-magnitudes using the Cardelli-89 extinction law.
n09_c3: \(C3\) Pseudo-color using the Nishiyama-09 extinction law.
n09_ab_color: Magnitude difference in the first epoch between the band \(a\) and the band \(b\) using the nishiyama-09 extinction law. Where \(a\) and \(b\) can be the bands \(H\), \(J\) and \(K_s\)
n09_m2 and n09_m4: \(m2\) and \(m4\) pseudo-magnitudes using the nishiyama-09 extinction law.
ppmb (Pseudo-Phase Multi-Band): This index sets the first time in phase with respect to the average time in all bands, using the period calculated by feets.
\[PPMB = frac(\frac{|mean(HJD_H, HJD_J, HJD_{K_s}) - T_0|}{P})\]Where \(HJD_H\), \(HJD_J\) and \(HJD_{K_s}\) are the time of observations in the band \(H\), \(J\) and \(K_s\); \(T_0\) is the time of observation of maximum magnitude in \(K_s\) band; \(mean\) calculate the mean of the three times, \(frac\) returns only the decimal part of the number, and \(P\) is the extracted period.
For more information about the extintion laws and pseudo colors/magnitudes:
Cardelli-89 Extinction law:
Cardelli, J. A., Clayton, G. C., & Mathis, J. S. (1989). The relationship between infrared, optical, and ultraviolet extinction. The Astrophysical Journal, 345, 245-256.
Nishiyama-09 Extinction law:
Nishiyama, S., Tamura, M., Hatano, H., Kato, D., Tanabé, T., Sugitani, K., & Nagata, T. (2009). Interstellar extinction law toward the galactic center III: J, H, KS bands in the 2MASS and the MKO systems, and 3.6, 4.5, 5.8, 8.0 μm in the Spitzer/IRAC system. The Astrophysical Journal, 696(2), 1407.
Pseudo colors/magnitudes:
Catelan, M., Minniti, D., Lucas, P. W., Alonso-Garcia, J., Angeloni, R., Beamin, J. C., … & Dekany, I. (2011). The Vista Variables in the Via Lactea (VVV) ESO Public Survey: Current Status and First Results. arXiv preprint arXiv:1105.1119.
Well lets play with the data of 3 Variable star
[4]:
rrs = df[df.vs_type == "RRLyr-RRab"][:3]
rrs
[4]:
| id | cnt | ra_k | dec_k | vs_type | vs_catalog | Amplitude | Autocor_length | Beyond1Std | Con | ... | c89_jk_color | c89_m2 | c89_m4 | n09_c3 | n09_hk_color | n09_jh_color | n09_jk_color | n09_m2 | n09_m4 | ppmb | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4456 | 32140000002913 | 68 | 280.582129 | -25.299033 | RRLyr-RRab | vizier | 0.12600 | 1.0 | 0.279412 | 0.0 | ... | 0.162897 | 13.827993 | 13.819663 | 0.053522 | 0.040231 | 0.123061 | 0.163291 | 13.893530 | 13.895081 | 1.629816 |
| 21827 | 32140000030432 | 68 | 280.482488 | -25.156328 | RRLyr-RRab | vizier | 0.17275 | 1.0 | 0.235294 | 0.0 | ... | 0.221322 | 13.112390 | 13.104045 | 0.049464 | 0.062893 | 0.158674 | 0.221566 | 13.185733 | 13.187114 | 1.672651 |
| 21929 | 32140000030564 | 68 | 281.279492 | -25.499744 | RRLyr-RRab | vizier | 0.18400 | 1.0 | 0.308824 | 0.0 | ... | 0.314535 | 14.001622 | 13.984766 | 0.128221 | 0.068086 | 0.246717 | 0.314803 | 14.087323 | 14.090839 | 2.006219 |
3 rows × 73 columns
We can check their mean of magnitudes to check if the source is not saturated or diffuse.
[5]:
rrs.Mean
[5]:
4456 14.086691
21827 13.488265
21929 14.412221
Name: Mean, dtype: float64
The three are between 12 an 16.5, so they are ok, and their pulsation?
[6]:
rrs.Std
[6]:
4456 0.071391
21827 0.090222
21929 0.120290
Name: Std, dtype: float64
Plotting time: we need the lc catalog to show the phased-folded light curve.
[7]:
lcs = client.get_catalog("b214", "lc")
Now to reduce the memory footprint we can retrieve the lc for only our 3 selected stars
[8]:
lcs = lcs[lcs.bm_src_id.isin(rrs.id)]
For make our code simple we can use to folde the light curve the PyAstronomy and numpy library
[9]:
from PyAstronomy.pyasl import foldAt
import numpy as np
[10]:
%matplotlib inline
import matplotlib.pyplot as plt
now we can plot the folded and unfolded lightcurves
[11]:
# get one ot the 3 sources
rr = rrs.iloc[0]
# retrieve the lightcurve for this rr
lc = lcs[lcs.bm_src_id == rr.id]
# sort by time
lc = lc.sort_values("pwp_stack_src_hjd")
# split in time, magnitude and error
time, mag, err = (
lc.pwp_stack_src_hjd.values,
lc.pwp_stack_src_mag3.values,
lc.pwp_stack_src_mag_err3.values)
# t0 is the first time
t0 = time[0]
# fold
phases = foldAt(time, rr.PeriodLS, T0=t0)
sort = np.argsort(phases)
phases, pmag, perr = phases[sort], mag[sort], err[sort]
# duplicate the values in two phases
phases = np.hstack((phases, phases + 1))
pmag = np.hstack((pmag, pmag))
perr = np.hstack((perr, perr))
# now create two plot for the folded and the unfolde LC
fig, axes = plt.subplots(2, 1, figsize=(12, 6))
# first lets plot the unfolded lc
ax = axes[0]
ax.errorbar(time, mag, err, ls="", marker="o", ecolor="red")
ax.set_title(f"Light Curve of source {rr.id}")
ax.set_ylabel("Magnitude")
ax.set_xlabel("HJD")
ax.invert_yaxis()
# now the folded lc
ax = axes[1]
ax.errorbar(phases, pmag, perr, ls="", marker="o", ecolor="blue", color="red")
ax.set_title(f"Folded Light Curve of source {rr.id}")
ax.set_ylabel("Magnitude")
ax.set_xlabel("Phase")
ax.invert_yaxis()
fig.tight_layout()
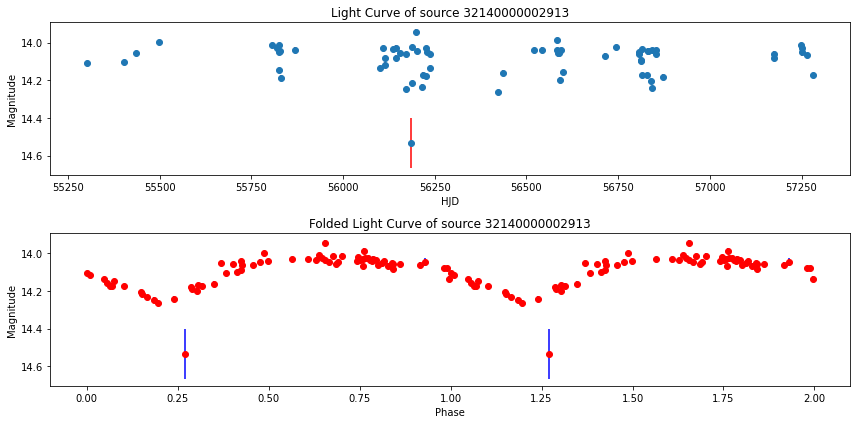
The next light curve
[12]:
rr = rrs.iloc[1]
lc = lcs[lcs.bm_src_id == rr.id]
lc = lc.sort_values("pwp_stack_src_hjd")
time, mag, err = (
lc.pwp_stack_src_hjd.values,
lc.pwp_stack_src_mag3.values,
lc.pwp_stack_src_mag_err3.values)
t0 = time[0]
phases = foldAt(time, rr.PeriodLS, T0=t0)
sort = np.argsort(phases)
phases, pmag, perr = phases[sort], mag[sort], err[sort]
phases = np.hstack((phases, phases + 1))
pmag = np.hstack((pmag, pmag))
perr = np.hstack((perr, perr))
fig, axes = plt.subplots(2, 1, figsize=(12, 6))
ax = axes[0]
ax.errorbar(time, mag, err, ls="", marker="o", ecolor="red")
ax.set_title(f"Light Curve of source {rr.id}")
ax.set_ylabel("Magnitude")
ax.set_xlabel("HJD")
ax.invert_yaxis()
ax = axes[1]
ax.errorbar(phases, pmag, perr, ls="", marker="o", ecolor="blue", color="red")
ax.set_title(f"Folded Light Curve of source {rr.id}")
ax.set_ylabel("Magnitude")
ax.set_xlabel("Phase")
ax.invert_yaxis()
fig.tight_layout()
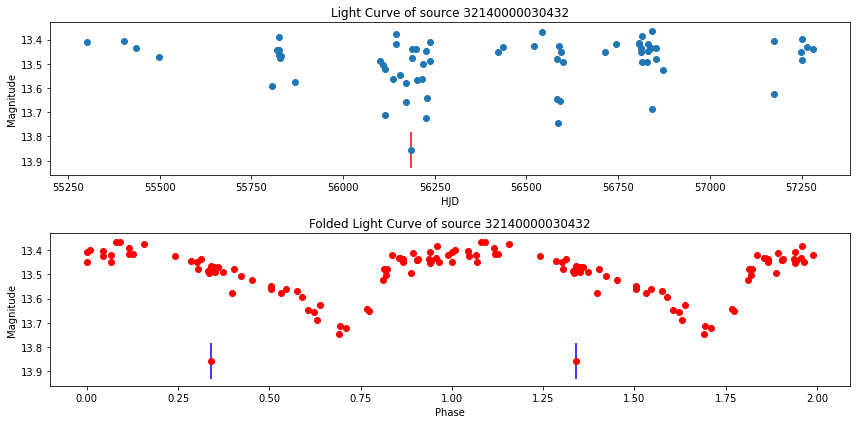
And the final one
[13]:
rr = rrs.iloc[2]
lc = lcs[lcs.bm_src_id == rr.id]
lc = lc.sort_values("pwp_stack_src_hjd")
time, mag, err = (
lc.pwp_stack_src_hjd.values,
lc.pwp_stack_src_mag3.values,
lc.pwp_stack_src_mag_err3.values)
t0 = time[0]
phases = foldAt(time, rr.PeriodLS, T0=t0)
sort = np.argsort(phases)
phases, pmag, perr = phases[sort], mag[sort], err[sort]
phases = np.hstack((phases, phases + 1))
pmag = np.hstack((pmag, pmag))
perr = np.hstack((perr, perr))
fig, axes = plt.subplots(2, 1, figsize=(12, 6))
ax = axes[0]
ax.errorbar(time, mag, err, ls="", marker="o", ecolor="red")
ax.set_title(f"Light Curve of source {rr.id}")
ax.set_ylabel("Magnitude")
ax.set_xlabel("HJD")
ax.invert_yaxis()
ax = axes[1]
ax.errorbar(phases, pmag, perr, ls="", marker="o", ecolor="blue", color="red")
ax.set_title(f"Folded Light Curve of source {rr.id}")
ax.set_ylabel("Magnitude")
ax.set_xlabel("Phase")
ax.invert_yaxis()
fig.tight_layout()
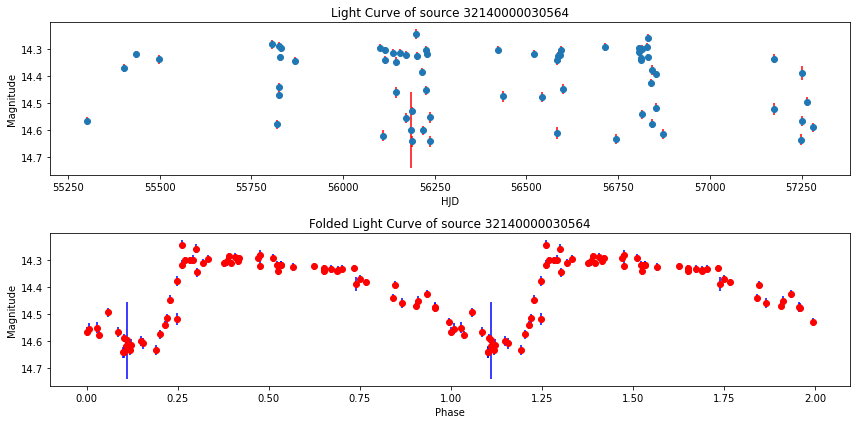
[14]:
import datetime as dt
dt.datetime.now()
[14]:
datetime.datetime(2022, 6, 13, 0, 13, 25, 563015)
[ ]: